有阻尼·单自由度系统的自由振动 | 小阻尼情况下
- 大阻尼和临界阻尼两种状态下,运动已无振动的性质;小阻尼情况下,系统振动不再是等幅的简谐振动,而是一种振幅按指数规律衰减的振动。其振动频率也是与初始振动无关,由系统的阻尼、刚度和质量确定,振动频率略小于无阻尼·单自由度系统的固有频率。
- 阻尼对自由振动的影响主要有两个方面:
- 一是阻尼使系统振动频率降低,周期略有增加。
- 二是振动按照指数衰减。阻尼越大,振幅衰减也愈快。
- 另外再补充一点,一般工程问题中,多属于小阻尼的情况,阻尼对系统的固有频率和周期的影响很小,因此在小阻尼的情况下,可以近似地认为有阻尼自由振动的频率和周期与无阻尼自由振动的频率和周期相等。
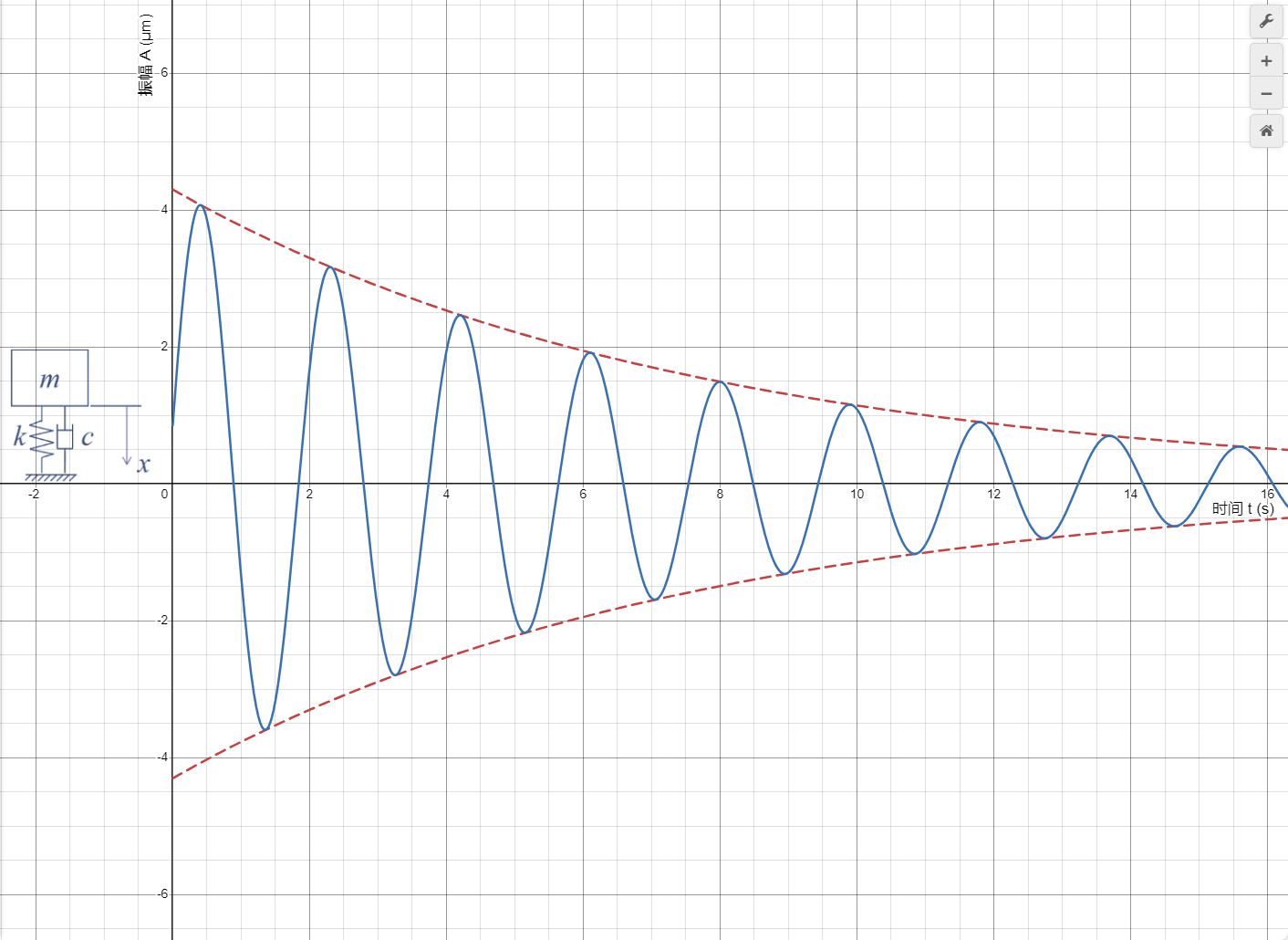
参数说明
\(m——质量\)
\(c——实际阻尼\)
\(k——刚度\)
\(A——振幅\)
\(𝝋——初相位\)
\(T——周期,无阻尼·单自由度系统的\)
\(𝒇——频率,无阻尼·单自由度系统的\),\(f=\frac1T\)
\(T_{1}——有阻尼·单自由度系统的振动周期\),\(T_{1}=\frac{\frac{2\pi}{\omega}}{\sqrt{1-\zeta^{2}}}\)
\(𝝎'——有阻尼·单自由度系统的固有频率\)
\(𝝎——无阻尼·单自由度系统的固有频率\),\(\omega=\sqrt{\frac{k}{m}}=2\pi{f}\)
\(c_{0}——临界阻尼系数\),\(c_{0}=2m\omega=2\sqrt{{k}{m}}\)
\(ζ——阻尼比\),\(\zeta=\frac{c}{c_{0}},系统实际阻尼与临界阻尼之比\)
上边界:\(Ae^{-\zeta\omega x}\left\{x>0\right\}\)
下边界:\(-Ae^{-\zeta\omega x}\left\{x>0\right\}\)
有阻尼·单自由度系统的自由振动:\(e^{-\zeta\omega x}\cdot A\sin\left(\sqrt{1-\zeta^{2}}\omega x+\varphi\right)\left\{x>0\right\}\)
无阻尼自由振动:\(A\sin\left(\omega x+\varphi\right)\left\{x>0\right\}\)


